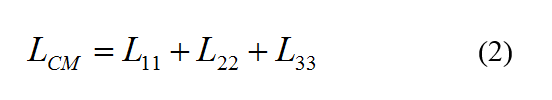Harness Development for Electromagnetic Compatibility Optimization of Power Conversion Chain for Aerospace
C. Jullien, E. Aubert, J. Genoulaz, A.Dieudonne
Abstract. This article presents an experimental validation of a harness distributing the filtering function and making the connection between a converter and a motor. This harness is both designed to have a common mode of reduced capacity and reduced shielding. This allows both to reduce the common mode current and the strain on power electronics. This offers weight reduction opportunities. Associated models are presented to simulate the entire power chain and provide validation.
I. Introduction
With the evolution of the "more electric aircraft", power management has assumed great importance in the development of new systems. The optimization of these sources and loads of these are essential to distribute the stresses. This will improve the material integrity of the system and its aging, while maintaining the aircraft specifications such as DO160 [1]. This optimization also involves the transmission of energy between two devices. The power chain derived from this application is presented in Figure 1:
- A DC power supply connected to the LISN (Line Impedance Stabilization Network
- Connect a three-phase static converter
- Converter connected to the motor via a power harness.
The LISN enables standardization for normative tests.
.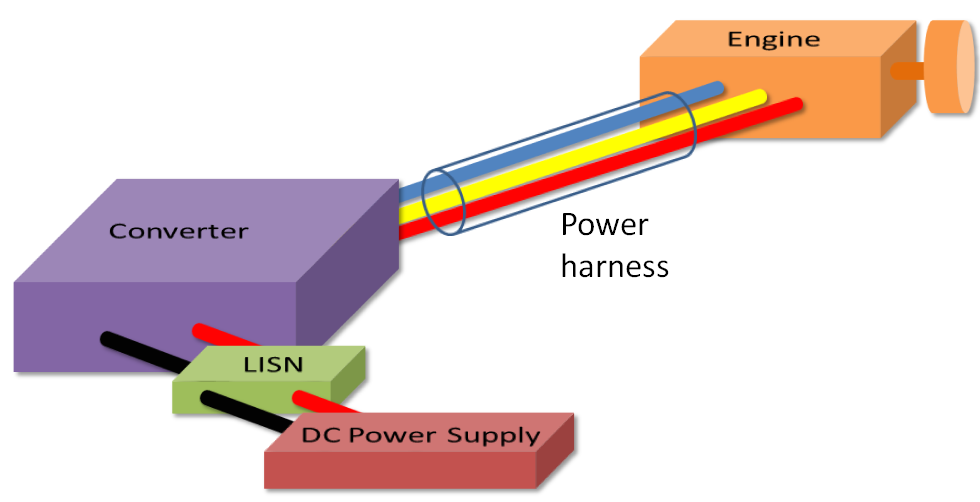
Figure 1. Principle of a power converter chain
The symmetrical DC power supply is connected to the converter by very short cables. The power harness, meanwhile, consists of a shielded three-wire cable which is of variable length but is how the energy is transmitted to the engine.
II. Harness optimization
II.1. Principle
The main problem derives from the inverter which drives the motor by a pulse width modulation using static switches. The high voltage variations generate a pulsed current in differential mode and common mode. To overcome this problem, manufacturers install filters at the converter. However, these filters are large, heavy and costly compared to that of the development of a power line.
Furthermore, to protect the environment from radiated emissions, a shield is required on the three-phase power line cable. It also represents a non-negligible impact on the design of the power line. For the harness, the parameters that have an impact on these constraints are placed on two levels:
- Common Mode capacitance of electrical harnesses: the common mode current stress brought to the harness depends largely on the common mode capacitance. To reduce this capacitance (common mode), move the shield.
- Overbraiding: if constraints require shielding, reduce the shield by degrading the transfer impedance in view of the common mode gain of the capacitance.
However, this study will be focused on improving common mode capability and functionality to the harness.
II.2. Simplified model of a power line
The “simplified” model of a power chain [2] uses common mode impedance measurements on different parts of the power chain (harness included). Using the theory of transmission lines through equivalent impedance and a Thevenin generator [3], calculate the common mode current on the phases at the inverter output. This principle is shown in Figure 2.
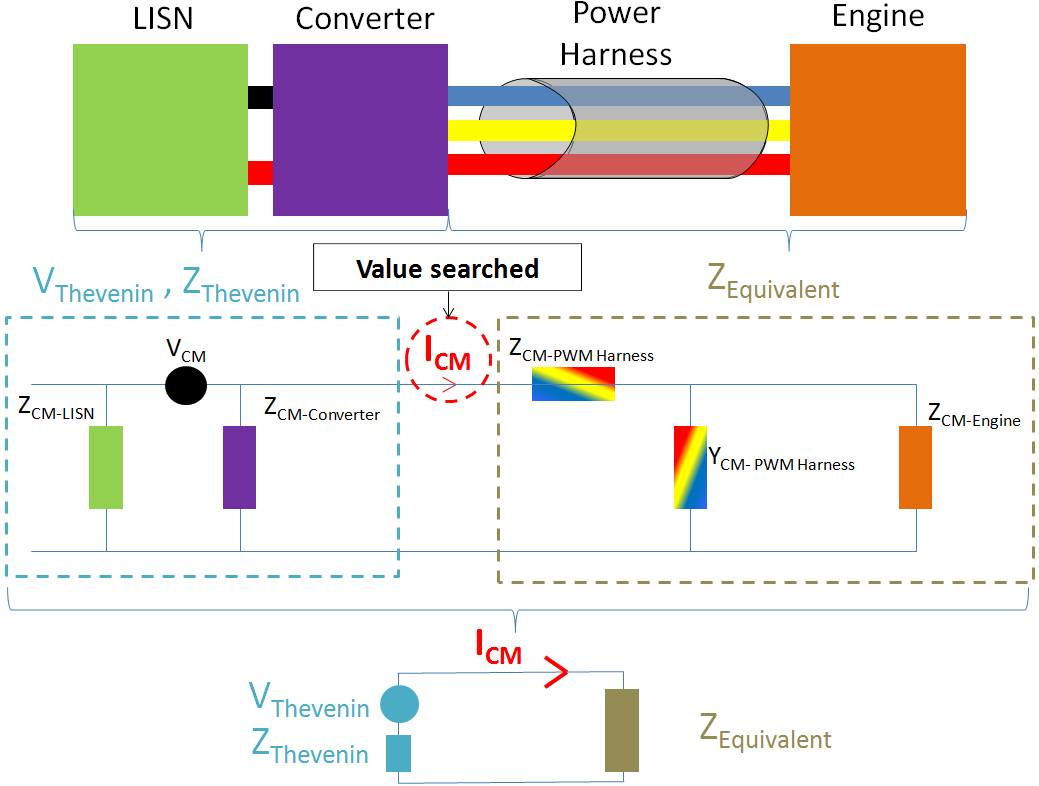
Figure 2. Principle of "simplified" model
It is a simple and easily implementable analytical method. It estimates the common mode current flowing in the three-phase inverter output. For this, it is necessary to have the common-mode impedance values of the equipment, which requires modeling (complex to model it) or a measurement on equipments (not always available depending on the phase).
II.3 Method to measure common mode impedance
To determine the common mode line parameters shielded three wire cable, the measurement protocol is to short circuit the phases at the two ends together and make two impedance measurements [4]. The first measurement is made between the shield and the grounding at one end. At the other end, the short circuit between phases is in open circuit with the shield. With this principle, directly measure impedance giving common mode capacitance (CCM) which is defined by the formula (1).
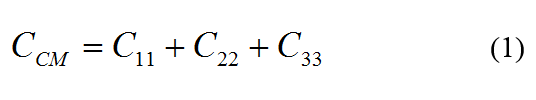
Capacitances between cables are not included in the measurement, thanks to short-circuit between phases.
The second step is to measure an impedance between the shield and the short-circuit of the three phases at any one end by shorting the 3 phases with the shield at the other end. With this principle, as before, directly measure impedance giving the common mode choke (LCM) defined by the formula (2).
II.4 Method to model power harness
The modeling protocol is to use the software CRIPTE [5] based on the electromagnetic topology applied to the transmission lines theory and developed by ONERA. The LAPLACE module takes into account a complex geometrical model of the harness. For this, it determines a quasi-static state by solving the Laplace equation for a linear capacitance matrix with and without insulation to derive the linear inductance matrix. The parameters for this calculation are the coordinates of the cables, the electrical reference and the permittivity of the insulation.
From these matrices of the linear parameters, build a topological network representing the power line as connected tubes and completed by junctions. Then take into account the load end in the junctions and the parameter lines in the tubes. This method provides current and voltage throughout the network whether complex or simple for a reasonable computation time and an industrial point of view.
This digital method is more complex than the previous one but considers harnesses for various geometries and especially enables modeling of the current and total common mode on the shield as defined in Figure 3.
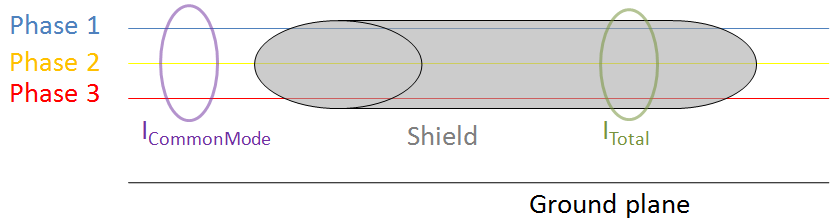
Figure 3. Definition of common mode current and total current
In addition, its iterative nature offers the possibility at performing parametric studies. Propagation phenomena can be fully taken into account because each tube is a uniform transmission line. Add as many tubes as are necessary to represent the random positions of the cables. That is, there a no constant distance between the three-phase cable and its shield.
To perform this study, we made the following approximations:
- The cross-section geometry of a three-wire twisted cable is constant relative to the shield
one tube to represent the harness.
- Neglect the impact of the link between the LISN and the filter converter. The interest of this study is in the link power behavior connecting the converter to the engine.
II.5 Comparison measurement / modeling common mode capacitance
Measures common mode impedances were performed with the HP4194A impedance analyzer, the 16047C module and a two-wire probe 12 gauge as shown in Figure 4.
Figure 4. Impedance analyzer
The case study concerns two 15m power harnesses. They consist of:
- A reference harness, a three-wire cable of gauge 4 with an overbraiding implementation.
- Enhanced capacitance harness, a three-wire cable of gauge 4 around which are placed 6 PTFE (PolyTetraFluoroEthylene) tubes of equivalent diameter, the whole being covered with a overbraiding.
The capacitance values have a constant frequency equal to resonance frequency. A survey was conducted to 100 kHz. The following table is obtained:
Congruence was observed in common mode capacitance between the measured values and the values obtained with LAPLACE. Considering the connectors in the estimation of the common mode (CM) capacitance equivalent harness improves results. The remaining difference can be explained by:
- Dimensional errors in the representation of the cross section
- Differences between the dielectric characteristics of the materials used
II.6. Comparison measurement / modeling with the simplified model and validations
From previously calculated and measured values, evaluate the impact of the cable with the simplified model. The results of model with the data of [2] are shown in Figure 5.
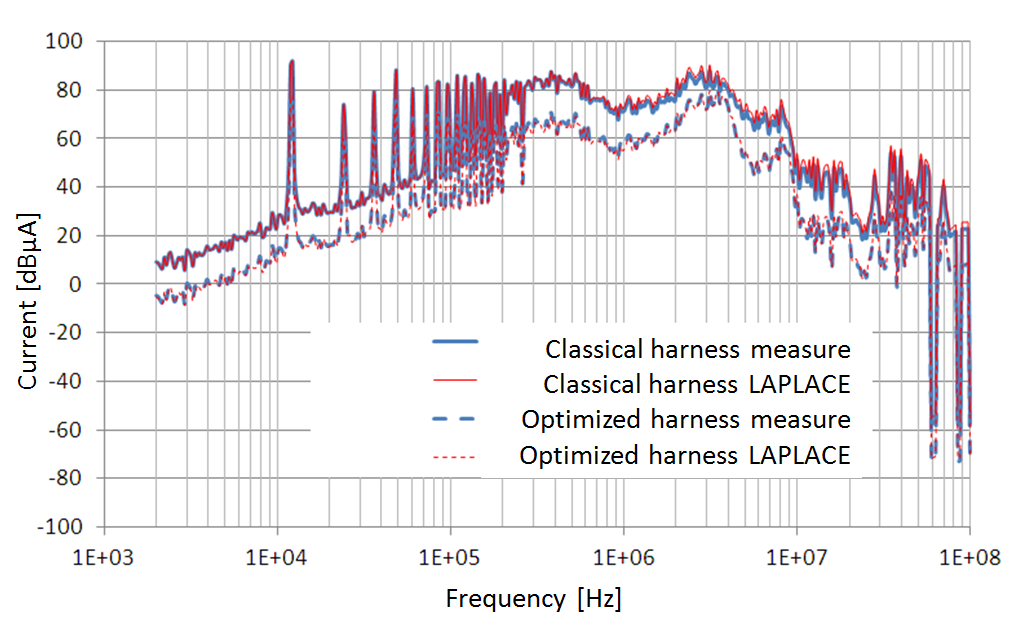
Figure 5. Common mode currents of reference harness and enhanced capacitance harness for measured and calculated values
Note that the small difference between the common mode capacitances between the measure and the model calculated with LAPLACE has little influence on the value of common mode current expressed in dBμA. The second observation relates to the gain provided by a spacing equivalent to a shielding conductor diameter. In fact, an average of 15dB reduction is observed over the entire frequency band from the reference harness. This decrease depends on the ratio of CM cable impedance compared to the impedances of CM equipment. When comparing the common mode current with the simplified model and simulation CRIPTE power chain, similar results are obtained as shown in Figure 6.
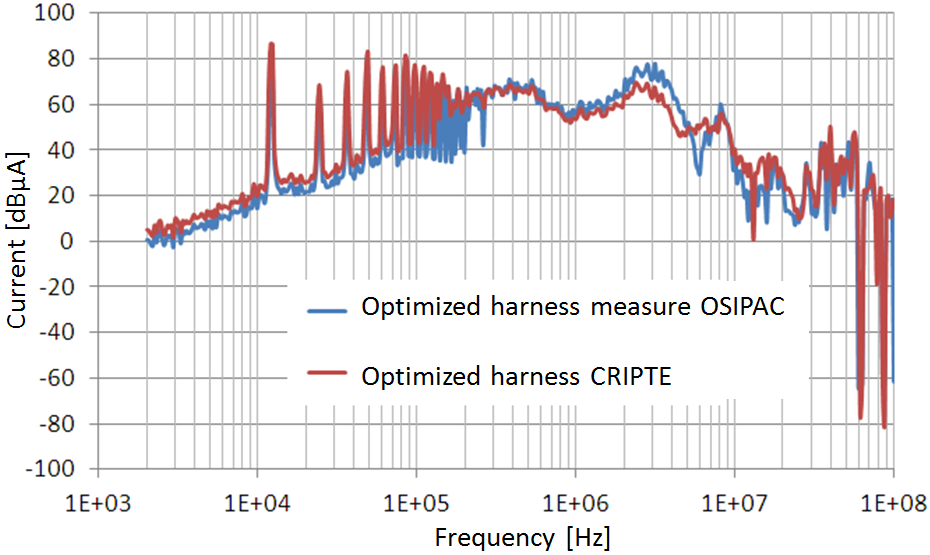
Figure 6. Common mode current with LAPLACE / CRIPTE and measurement / Model Simplified
III. APPLICATION TO A GLOBAL POWER CHAIN
III.1 Introduction
The numerical and experimental validations of the previous section show the rationale for removing the cable shield in order to reduce common mode. Simulations support the phase common mode reduced current. Previous harnesses have been developed for application of several tens of kW but could not be included for reasons of availability of the test bench. The application on a real case of power chain was carried out on a test bench of a dozen kW allowing the integration of an enhanced capacitance harness dimensioned for this power level.
III.3 Presentation of the test bench
The test bench consists of a power supply, two LISNs, the converter provided with a location for an output filter, a ground plane with shims to accommodate a harness and a motor. It was provided by Safran Electrical & Power, Div. Power. Two measurements are made:
- A common mode current upstream of the converter EMC filter on the three representative phases of the simplified model
- A total current on the shield harness outflow of converter standard
The samples tested were a "classic" harness and a harness "optimized", 10m long each. This bench is shown in Figure 7.

Figure 7. Test bench of Safran Electrical & Power Div. Power
These harnesses are both composed of a three-wire cable gauge 16. The conventional harness is composed of a shielded cable wrapping. The optimized harness has 6 equivalent diameters of polyamide tubes for the three-wire cable on which an overbraid is placed. This shield is also lightweight in the sense that a number of strands are textile.
Indeed, reducing the common mode current causes a decrease in total current and thus the power radiated by the shielding. Thus the stress on the transfer impedance can be relaxed in favor of a reduction of the mass of shielding. To exhibit this, reduce the number of wire strands used in the braiding of the harness.
III.3 LAPLACE modeling and simulation by the simplified model
To model the two harnesses, use the same LAPLACE parameter lines matrices. However, the conventional harness can be modeled as done previously regardless of a ground plane. Consider that the hypothesis called "good shielding" is valid in this case. For an optimized harness, use two models considering the hypothesis mentioned above and the other using the strands layers as conductors of equivalent diameters placed above a ground plane. These models are shown in Figure 8.
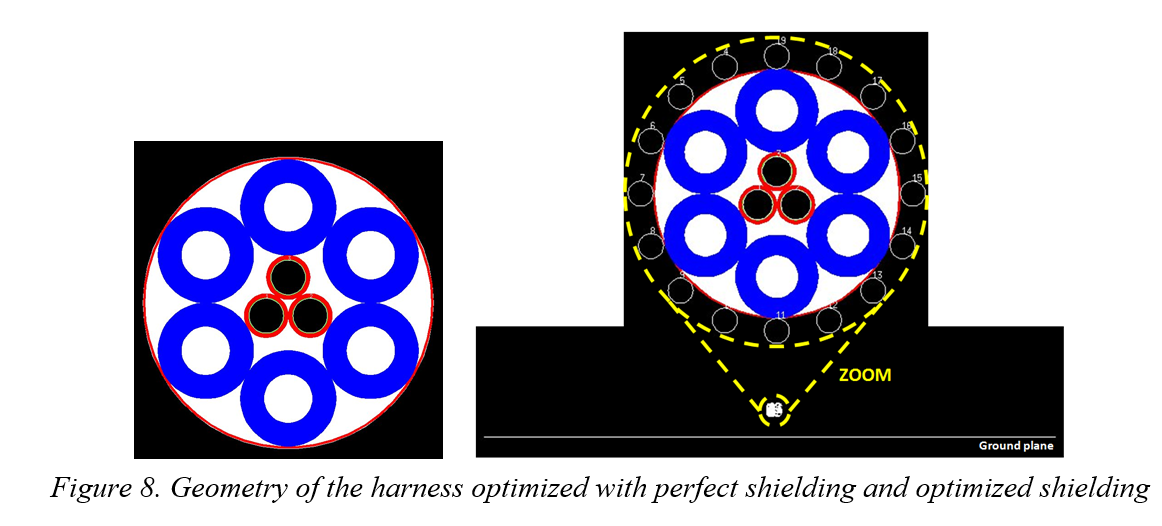
Observe that the difference between the optimized cable and the conventional cable is less important than in the case of previous study. This is explained by the presence of polyamide tubes which have a permittivity approximately two times greater than that of PTFE.
If we use these values with the simplified model, the results presented are obtained in Figure 9.
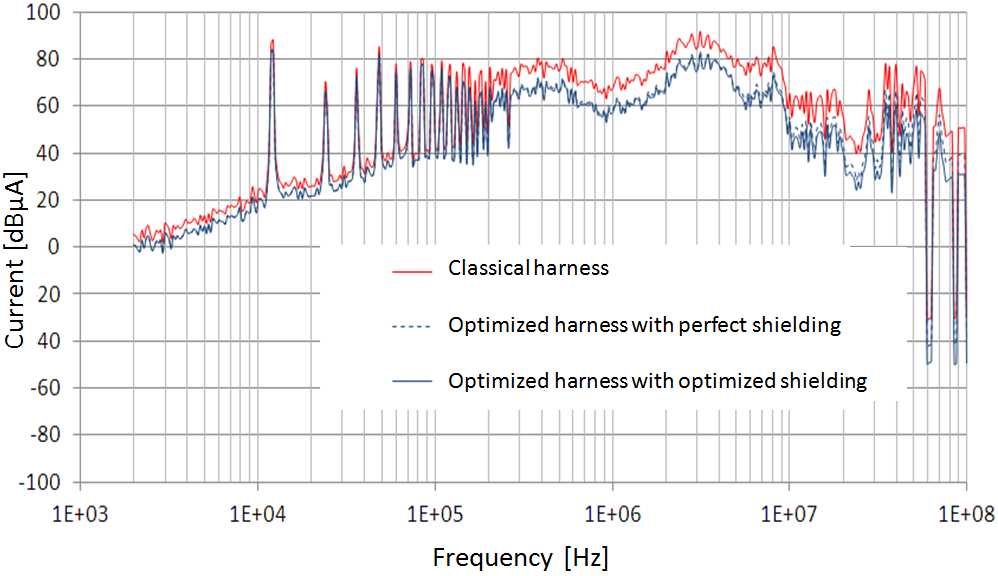
Figure 9. Common mode current for conventional and optimized harness with perfect shielding and optimized shielding
Note here that the average difference between conventional harness and optimized harness with lightweight shield is about 10dB. However, the difference between the perfect shielding and shielding lightened for optimized harness is less than 2dB.
III.4 Measurement results
The first measure consists of the common mode output current without a filter converter. A comparison can be made between the classical harness and an optimized harness with a lightweight shield. The results are shown in Figure 10.
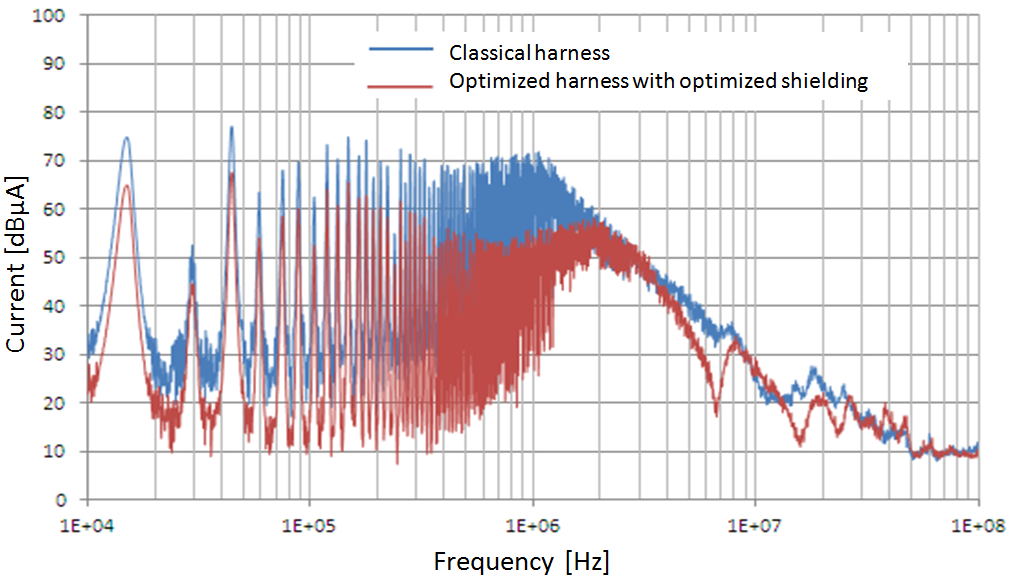
Figure 10. Common mode current without filter for conventional and optimized harness with perfect shielding and optimized shielding
Note here that the average difference in CM current for both harnesses is 10dB as seen with the simplified model. The filter is removable which makes it possible to test two configurations: standard with optimized filter and without the filter. The results are shown in Figure 11.
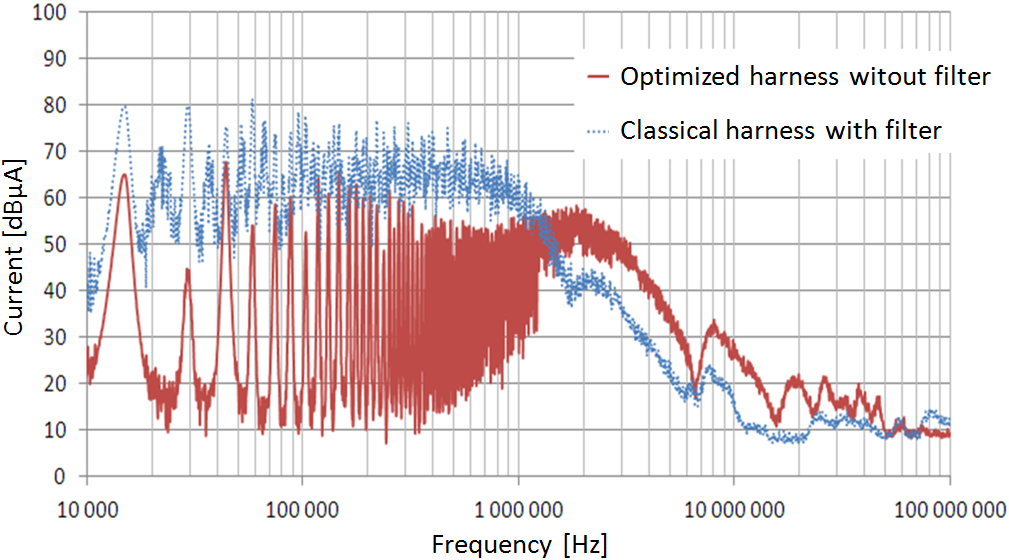
Figure 11. Common mode current for conventional harness with filter and optimized harness without filter
We observe that on average we gain 15dB over the frequency range 10kHz-1MHz. The filter is a simple inductive coil, it has a capacitive behavior from 1MHz which explains the high frequency performance decrease.
The second measure gives the total current on the shield of the harness. The results are shown in Figure 12.
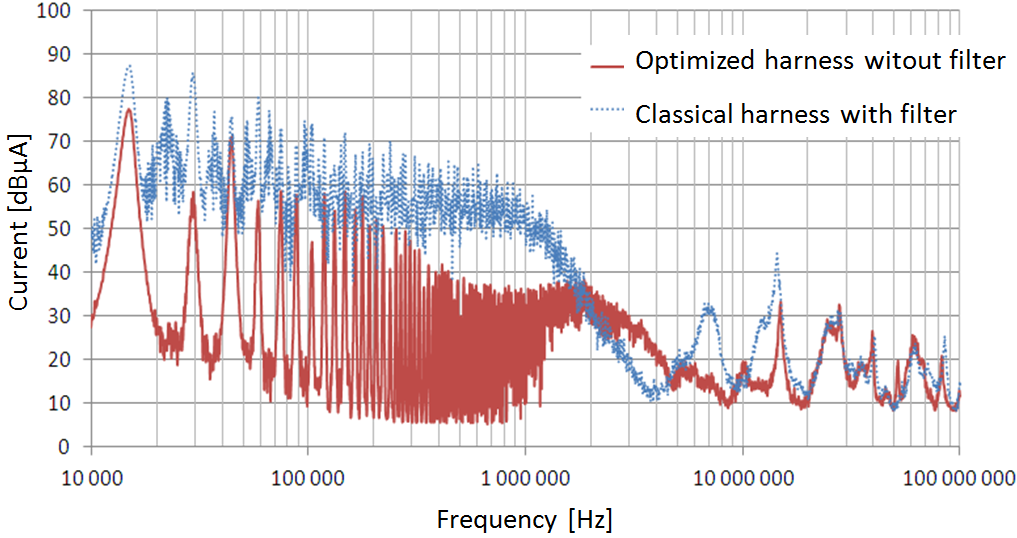
Figure 12. Global current for conventional harness with filter and optimized harness without filter
Note the improvement of an average 20 dB over the entire frequency band except between 2 and 5 MHz. It is observed that optimizations allow significant gain over the total current.
The overall results show a non-negligible gain on some or the entire frequency band. Although the mass of the harness increases due to the spacer, the lightweight shielding partially offsets the extra weight in the harness.
IV. CONCLUSIONS
In conclusion, the results of measurements and models validate the improvements made to the dimensioning of the power harness. Indeed, by spacing the shielding from the three wires, it can reduce the common mode current constraint and therefore make it possible to consider removal of the filter in the converter. In addition, a simplified model can predict the behavior of the common mode current harness.
Further work should allow optimization of the spacer dimensions between the shield and the three wires and the lightened shield. A study of the design of the filter function between the harness and the EMC filter of the converter allows estimation of the weight savings on the overall system.
REFERENCES
[1] RTCA DO160, "Environmental Conditions and Test Procedures for Airborne Equipment".
[2] M. Dunand, L. Kone, H. Moussa, "Méthode d’optimisation de câbles pour des dispositifs de conversion de puissance", CEM 2012, Rouen
[3] F. Costa, C. Gautier, B. Revol, J. Genoulaz, B. Demoulin, "Modeling of the Near-Field Electromagnetic Radiation of Power Cables in Automotives or Aeronautics", Power Electronics, IEEE Transactions on, vol. 28, n. 10, pp. 4580-4593, March 2013.
[4] P. Degauque, A. Zeddam, "Compatibilité électromagnétique Volume 2", Ed. Hermes, 2007
[5] J.P. Parmantier, S. Bertuol, “CRIPTE: User guide”, s.l. : ONERA/DEMR -009/06 – S,2006. Vol. CRIPTE 4.2
Biographies:
 |
Charles Jullien (M’10) was born in 1985, in Rodez, France. He received the Master’s Degree in computational physics from Université des Sciences de Montpellier and the Ph.D. degree in electronics and telecommunication from the Institut d’Electronique et de Telecommunications de Rennes in 2013. Since November 2012, he is currently with Safran Electrical & Power, Blagnac, France. He is working in the EMC team of R&T Department of EWISe Division and, since 2015, he is currently expert society in EMC electrical harness modeling. His research interest includes modeling electromagnetic coupling in aeronautical harness and over shielding harnesses. |
 |
Eddy Aubert was born on 31 July 1980 in Orléans, France. He received the University master degree in electrical engineering in Paul Sabatier University in Toulouse. He joined the LAboratory of PLasma and Energy ConvErsion -LAPLACE- in Toulouse and obtained his PhD degree in electrical engineering in 2008 from Paul Sabatier University. He entered in aeronautical industry domain and he joined Safran group in 2012. He is now dealing with aeronautical high voltage and high electrical power for Electrical Wiring Interconnection Systems - EWIS. He is concerned in the relationship between experiments and simulations. He is currently expert society in Safran Electrical & Power in wiring and interconnection aeronautical high voltage.
|
 |
Jérôme Genoulaz was born in France, in 1978. He received the M.S. degree in electrical engineering from Ecole Normale Supérieure de Cachan, in 2005, and the Ph.D. degree in electrical engineering from the University of Lille, in 2008. He is currently with SAFRAN Electrical & Power, Blagnac. He is the Head of Advanced Research in the R&T Department of EWISe Division. His research interests include power electronics interferences, shielded cable and over shielding harnesses, protection against lightning indirect effects, power line communication, and health monitoring of electrical wiring interconnection systems.
|
 |
Anca Dieudonné received the electrical engineering degree from the “Politehnica” University of Timisoara, Timisoara, Romania, in 2007, the Research Master degree and the Ph.D. degrees in electrical engineering from the “Institut National Polytechnique de Grenoble,” Grenoble, France, in 2008 and 2012, respectively. She joined Safran Electrical & Power, in 2008, for the master internship. Since then she has been with the R&T Department of EWISe Division, Safran Electrical & Power. Now she is the Head of EMC, Lightning and Modelization team in the R&T Department of EWISe Division, Safran Electrical & Power. Her current research interests include low-frequency full-wave modeling aspects of electrical networks, current return networks in composite aircrafts, and optimization of large-scale.
|
About the Newsletter
Editors-in-Chief

Jin-Woo Ahn
Co-Editor-in-Chief

Sheldon Williamson
Co-Editor-in-Chief
TEC Call for Articles 2023 - Advances in Charging Systems
The TEC eNewsletter is now being indexed by Google Scholar and peer-reviewed articles are being submitted to IEEE Xplore.
To submit an article click here.