Sliding Mode Control (SMC) in Control of Unmanned Aerial Vehicles (UAVs)

by

Kalyani Mamidi, Jayati Dey & Subrata Banerjee*
Department of Electrical Engineering, NIT Durgapur, Durgapur 713209, India

Abstract: In recent eras, Unmanned Aerial Vehicles (UAVs) are being deployed in many real-world tasks. More specifically, it is observed that multi-rotor copters are an alternative substitute for manned or fixed-wing aircraft UAVs in multi-purpose applications, including civil, defense, and military operations. These jobs are accomplished under challenging environments where aerodynamic influences, uncertainties, and nonlinear dynamics play a dominant part. Hence precise control of such vehicles is becoming a job of significant importance day by day. Robust nonlinear control is demanded in order to cope with these undesired situations. A thorough review of the literature establishes Sliding mode Control (SMC) to be a well-proven solution to control UAVs. In near future, adaptive PID SMC can be a reasonable choice for implementation to UAVs for efficient and cost-effective operation.

 

Introduction

Unmanned aircraft systems (UAS), commonly known as multi-rotor drones, are a rapidly growing sector of aerospace industries. They are being developed for several notable applications including military and defense missions such as surveillance and border patrol, search and rescue tasks, civilian works like precision agriculture, inspection and monitoring, data collection, payload carrying and delivery, etc. The significant advantages of these Unmanned Aerial Vehicles (UAVs) over helicopter systems are their low cost, simpler configuration, miniature size, vertical landing and take-off (VTOL) capability, hovering ability, and ease of maintenance. In recent days, with the advancement of technology, researchers are going on to develop reliable, safe, hazardless, and optimum power-consuming operations of UAS for mission-oriented applications. 

A multi-rotor drone is an under-actuated multi-input-multi-output (MIMO) system in which the control inputs regulate the three translational and three rotational motions changing of the speed of the rotors for different maneuvers, hovering, take-off, and landing [1]-[3]. It is highly unstable due to aerodynamic effects, non-linear dynamics, continuous parameter variation, time-varying states and delays, and therefore, its attitude and altitude control are of immense importance and a challenging job. There are many motivating problems for UAVs, such as mathematical modeling of mechanical parts, control and stabilization, precise landing, path planning, state estimation, and battery management. The strong research focuses are on UAV operations in mountainous terrain, unavoidable aerodynamic turbulence, and environments for which prior information are not available. Operations under such adverse situations demand precise flight control and navigation, obstacle avoidance, autonomous planning, perception and decision-making, robust state estimation, health maintenance, and a high-level interface for human-robot interaction. It is desired to design an efficient controller for set point tracking penetration of all the linear positions and attitudes under these unwanted situations.

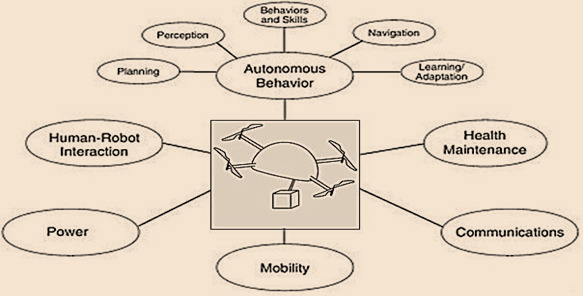
Fig. 1. Area of technology Needed for UAVs

To achieve the desired tracking performance even in presence of these unavoidable circumstances, several classical and adaptive control techniques have been proposed in literature which include, feedback linearization controls [4], linear and adaptive proportional-integral-derivative (PID) controls [5], model predictive control (MPC) [6], intelligent, adaptive, optimal and robust controls [7]-[9], backstepping control [10]-[11], sliding-mode control (SMC) [12]-[14].

In near future, UAVs will be operated in numerous complicated missions which will utilize their competence to (I) work in the vicinity of the populated environment with obstacles, (II) be robust to adverse atmospheric environments, and (III) ensure the safety of their payloads under faulty conditions. These stringent necessities can be met with nonlinear robust control algorithms to design efficient autopilots. Sliding Mode Control (SMC) is a technique that allows one to design controllers for complex nonlinear systems. Classical and extended SMC are widely accepted for ensuring robustness to complicated dynamic environments, by virtue of their inherent ability to work in presence of unknown uncertainties and disturbances. Moreover, the extended high-order SMC can overcome its well-known disadvantage of the chattering phenomenon. A literature review reveals some works on SMC applied for multi-rotor drones [12]-[14]. In this article, a brief review on designing SM controllers is presented.

A) PD Sliding Mode Control:

Here the sliding surface s(t) is chosen as proportional and derivative form of the error function (t), which is the error between desired and actual for the control variable.  

Where λ>0 is a tuning parameter. The sliding mode control U(t), involves two parts: an equivalent part, u_eq(t), which is continuous whereas the 2nd part is a discontinuous denoted by u_D(t).   u_eq(t)  is a function of each of the state variables which is needed to be controlled, and its corresponding desired value. On the other hand, u_D(t) is the sliding surface which is nonlinear in nature and acts as a switching element. k_D is a gain to be set which is responsible for reaching phase. The chattering problem can be reduced by such a choice of the control law.

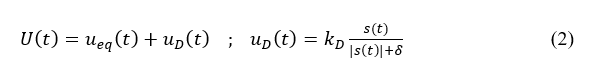
δ is a tuning parameter that is responsible for the reduction in the chattering effect. To design u_D(t), a Lyapunov function V is defined as 0.5s². The reaching condition is given by V<0.  In order to satisfy it, one requires k_d>0.

B) PID Sliding Mode Control:

PD sliding surface fails to reject disturbances. Therefore, an integral sliding surface is introduced to the PD sliding Surface. Hence, it can be re-written as:

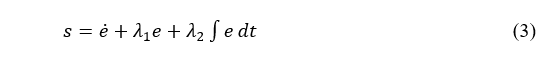
Where λ1,λ2 are tuning parameters required to be greater than zero for a stable response. 

C) Adaptive Sliding Mode Control:

An adaptive method is capable to predict the upper bounds of unknown disturbances. The design procedure of the adaptive parameter-tuning algorithm may be expressed as follows:

Consider external disturbances of unknown nature but bounded magnitude while k_D (>0) in (15) is an unknown coefficient. The PID sliding surface is expressed as previously as (3). The tuning parameter k_D is adopted to predict k_D . The error of approximation is given by k_D=k_D-k_D,desired and Lyapunov function V is defined as 0.5S²+0.5 μk_D². In order to obtain V(t) < 0, the adaptive law will be deduced.

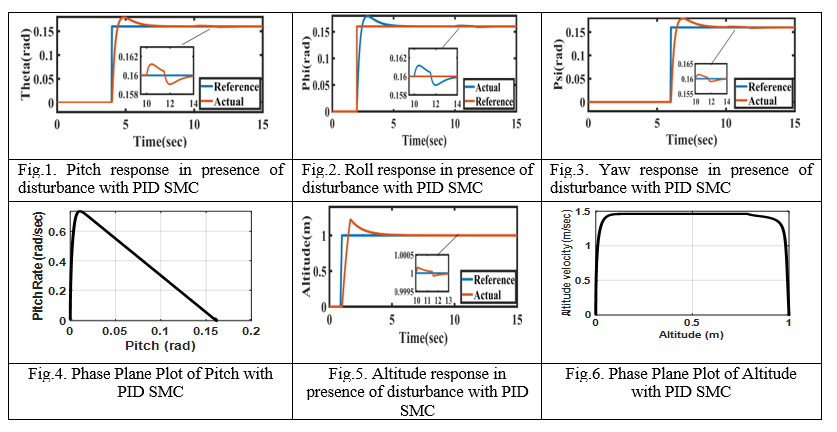
Some Results

The reference values are considered to be z_d = 1m, Roll ϕ_d=5°, Pitch θ_d=5°, Yaw ψ_d=5°. An external disturbance is introduced during a simulation at time 10s. 

V. Conclusion

Quadcopters, due to their vertical take-off and landing ability, high maneuverability, and compact size, have gained immense popularity in precision agriculture, surveillance, geographical explorations, etc. As it is a non-linear, under actuated and highly unstable complex system, it is quite challenging to design its suitable mathematical model and control it autonomously. As the technology is moving towards more nonlinear and robustness, the SM control yields a satisfactory tracking performance even in presence of disturbances. Future studies on adaptive second-order SMC may further lead to improvement in the robustness of the system.

References

[1] H. Liu, J. Xi, and Y. Zhong, “Robust attitude stabilization for nonlinear quadrotor systems with uncertainties and delays”,  IEEE Trans. Ind. Electron., vol. 64, no. 7, pp. 5585-5594, Jul. 2017.
[2] Z. A. Ali and X. Li, “Controlling of an under-actuated quadrotor UAV equipped with a manipulator”, ' IEEE Access, vol. 8, pp. 34664-34674, 2020.
[3] M. Rabah, A. Rohan, S. A. S. Mohamed, and S.-H. Kim, “Autonomous moving target-tracking for a UAV quadcopter based on fuzzy-PI,  IEEE Access, vol. 7, pp. 38407-38419, 2019.
[4] D. Lee, H. J. Kim, and S. Sastry, “Feedback linearization vs. adaptive sliding mode control for a quadrotor helicopter”,  Int. J. Control, Automat. Syst., vol. 7, no. 3, pp. 419-428, 2009. 
[5] P. E. I. Pounds, D. R. Bersak, and A. M. Dollar, “Stability of small-scale UAV helicopters and quadrotors with added payload mass under PID control”,' Auton. Robots, vol. 33, nos. 1-2, pp. 129-142, 2012.
[6] K. Alexis, G. Nikolakopoulos, and A. Tzes, “Model predictive quadrotor control: Attitude, altitude and position experimental studies”, IET, Control Theory Appl., vol. 6, no. 12, pp. 1812-1827, Aug. 2012.
[7] T. Lee, “Robust adaptive attitude tracking on SO(3) with an application to a quadrotor UAV”,  IEEE Trans. Control Syst. Technol., vol. 21, no. 5, pp. 1924-1930, Sep. 2013. 
[8] L. Wang and J. Su, “Robust disturbance rejection control for attitude tracking of an aircraft”,  IEEE Trans. Control Syst. Technol., vol. 23, no. 6, pp. 2361-2368, Nov. 2015.
[9] D. Cabecinhas, R. Naldi, C. Silvestre, R. Cunha, and L. Marconi, “Robust landing and sliding maneuver hybrid controller for a quadrotor vehicle”,  IEEE Trans. Control Syst. Technol., vol. 24, no. 2, pp. 400-412, Mar. 2016.
[10] Z. Zuo and S. Mallikarjunan, “L1 Adaptive backstepping for robust trajectory tracking of UAVs”,' IEEE Trans. Ind. Electron., vol. 64, no. 4, pp. 2944-2954, Apr. 2017.
[11] F. Chen, R. Jiang, K. Zhang, B. Jiang, and G. Tao, “Robust backstepping sliding-mode control and observer-based fault estimation for a quadrotor UAV,'' IEEE Trans. Ind. Electron., vol. 63, no. 8, pp. 5044-5056, Aug. 2016.

Authors

	Kalyani Mamidi received a Bachelor's degree in Electrical and Electronics Engineering from Andhra University, Visakhapatnam in year 2018, and the degree of Master of Technology in Electrical Engineering, with a specialization in Power Electronics and Machine Drives, from the National Institute of Technology, Durgapur, in 2022. I am currently working in Smart SoC Solutions and Pvt. Ltd. as Physical Design Engineer in the VLSI domain in Hyderabad.
	Jayati Dey (M’09-SM’22) received the degree of Bachelor of Electrical Engineering in 2000 from Jadavpur University, Kolkata, a Master of Engineering in 2003 from Bengal Engineering College, Shibpur, and a Doctor of Philosophy degree in 2007 from IIT Kharagpur, India. She is currently serving as an Associate Professor in the Department of Electrical Engineering, National Institute of Technology Durgapur, India. Her research interests are periodic compensation, switching power converters, robotics and mechatronics, and Unmanned Vehicles, with a special interest in robust control. She has authored about 75 research papers in international journals and conferences.
	Subrata Banerjee (M’04–SM’15) is working as Professor with the Department of Electrical Engineering, National Institute of Technology, Durgapur, India. His research interest includes modeling & control of switch-mode converters and inverters, multilevel inverters & different modulation techniques, electromagnetic levitation, active magnetic bearing, controller design, intelligent control, etc. He is a Fellow of IE (India), the IETE (India), and the IET (UK), Senior Member of IEEE (USA). He is acting as Associate Editor/Editorial Board in IEEE Access (USA), IET Power Electronics (UK)/ IEEE Transportation Electrification Community eNewsletter (USA), and Transportation Electrification (specialty section of Frontiers in Future Transportation).